Βασική διαφορά: Ένας κύκλος και η ελλειψία έχουν κλείσει καμπύλα σχήματα. Σε έναν κύκλο, όλα τα σημεία είναι εξίσου μακριά από το κέντρο, πράγμα που δεν συμβαίνει με έλλειψη. σε έλλειψη, όλα τα σημεία βρίσκονται σε διαφορετικές αποστάσεις από το κέντρο.
Μαθηματικά, ένας κύκλος είναι ένα σημαντικό σχήμα στο πεδίο της γεωμετρίας και ο ορισμός του ορίζεται: ένας κύκλος είναι ένα σχήμα με όλα τα σημεία στην ίδια απόσταση από το κέντρο του. Ονομάζεται από το κέντρο της. Ορισμένα παραδείγματα πραγματικού κόσμου ενός κύκλου είναι οι τροχοί, η πλάκα δείπνου και (η επιφάνεια) ένα νόμισμα.
Η λέξη « τσίρκο » προέρχεται από τον ελληνικό όρο « kirkos », ο οποίος είναι μια μετάθεση του ομηρικού ελληνικού και σημαίνει « δαχτυλίδι » ή « δαχτυλίδι ». Ο κύκλος ήταν γνωστός πριν από την καταγραφή του ιστορικού. Ο ήλιος και η Σελήνη είναι φυσικά παραδείγματα ενός κύκλου, ενώ ακόμη και ένα μικρό μίσχο που φυσάει στον άνεμο, σχηματίζει το σχήμα ενός κύκλου στην άμμο. Η αρχή ενός κύκλου εφαρμόστηκε στο σχηματισμό τροχών και εργαλείων από τον προϊστορικό άνθρωπο. Τώρα στη σύγχρονη εποχή, υπάρχουν αναρίθμητες ποικιλίες μηχανημάτων με βάση το σχήμα του κύκλου. Η μελέτη ενός κύκλου και η ανάπτυξή του είναι εφαρμόσιμη στους τομείς των μαθηματικών, της γεωμετρίας, της αστρονομίας και του λογισμικού.
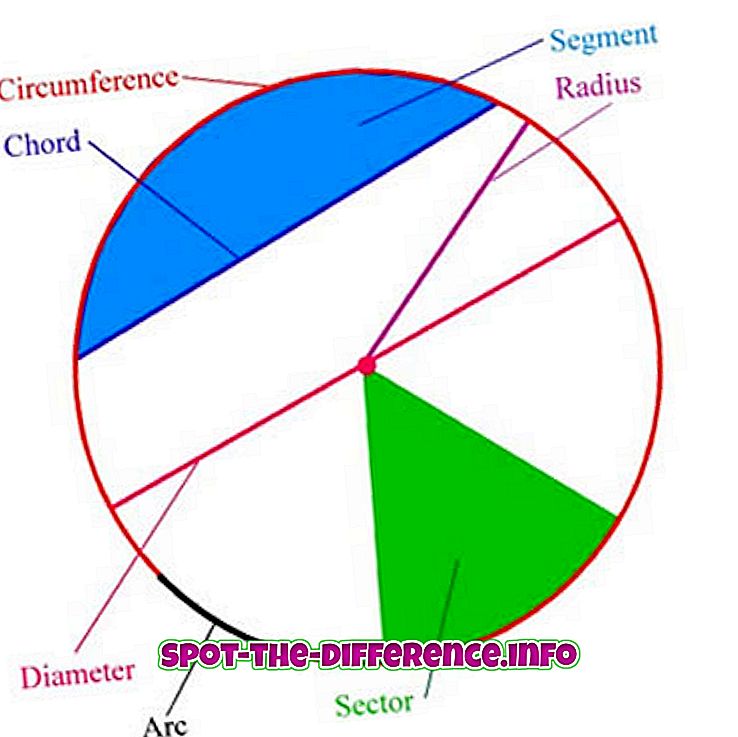
Οι παρακάτω όροι εμπλέκονται στην ορολογία κύκλου:
Arc : κάθε συνδεδεμένο μέρος του κύκλου.
Κέντρο : Το σημείο είναι ίσο από τα σημεία του κύκλου.
Ακτίνα : ένα τμήμα γραμμής που ενώνει το κέντρο του κύκλου με οποιοδήποτε σημείο του ίδιου του κύκλου. ή το μήκος ενός τέτοιου τμήματος, το οποίο έχει μισή διάμετρο.
Διάμετρος : ένα τμήμα γραμμής του οποίου τα τελικά σημεία βρίσκονται στον κύκλο και το οποίο διέρχεται από το κέντρο. ή το μήκος ενός τέτοιου τμήματος γραμμής, το οποίο είναι η μεγαλύτερη απόσταση μεταξύ οποιωνδήποτε δύο σημείων στον κύκλο. Είναι μια ειδική περίπτωση μιας χορδής, δηλαδή της μακρύτερης χορδής, και είναι διπλάσια από την ακτίνα.
Περίπτωση e: το μήκος ενός κυκλώματος κατά μήκος του κύκλου.
Χορδή : ένα τμήμα γραμμής του οποίου τα τελικά σημεία βρίσκονται στον κύκλο.
Έμφυτη : μια ομοεπίπεδη ευθεία που αγγίζει τον κύκλο σε ένα μόνο σημείο.
Semicircl e: μια περιοχή που οριοθετείται από μια διάμετρο και ένα τόξο που βρίσκεται ανάμεσα στα τελικά σημεία της διαμέτρου. Πρόκειται για μια ειδική περίπτωση ενός κυκλικού τμήματος, δηλαδή του μεγαλύτερου.
Κυκλικός τομέας : μια περιοχή που οριοθετείται από δύο ακτίνες και ένα τόξο που βρίσκεται μεταξύ των ακτίνων.
Μαθηματικά, μια έλλειψη είναι ένα κοινό σχήμα στον τομέα των μαθηματικών. Ο ορισμός του δηλώνει: μια καμπύλη γραμμή που σχηματίζει έναν κλειστό βρόχο, όπου το άθροισμα των αποστάσεων από δύο σημεία (εστίες) σε κάθε σημείο της γραμμής είναι σταθερό. Τα παραδείγματα αληθινής ζωής μιας ελλείψεως είναι: ένα χούλα χούπα, ένα ποτήρι νερό και μια απλή πλάκα δείπνου όταν γέρνουν για να βλέπουν υπό γωνία.
Ο Απόλλωνιος της Πέργας έδωσε το όνομα «έλλειψη» στα Conics του, το οποίο τονίζει τη σύνδεση μιας καμπύλης με την εφαρμογή περιοχών. Είναι μια καμπύλη σε ένα επίπεδο που περιβάλλει δύο εστιακά σημεία, έτσι ώστε μια ευθεία που τραβιέται από ένα από τα εστιακά σημεία σε οποιοδήποτε σημείο της καμπύλης και στη συνέχεια πίσω στο άλλο εστιακό σημείο έχει το ίδιο μήκος για κάθε σημείο της καμπύλης. Το σχήμα του αντιπροσωπεύεται από την εκκεντρότητα του, η οποία είναι αυθαίρετα κοντά στο 1. Η μελέτη της ελλειψίας και οι ιδιότητές της ισχύουν συνήθως στον τομέα της φυσικής, της αστρονομίας και της μηχανικής. Οι τροχιές των πλανητών με τον Ήλιο σε ένα από τα σημεία εστίασης, τα φεγγάρια γύρω από τους πλανήτες και άλλα συστήματα που έχουν δύο αστρονομικά σώματα είναι τα γενικά παραδείγματα ελλειπτικών μονοπατιών. Το σχήμα των πλανητών και των αστεριών συχνά περιγράφεται καλά από τα ελλειψοειδή. Η έλλειψη θεωρείται επίσης ως η απλούστερη μορφή Lissajous, που σχηματίζεται όταν οι οριζόντιες και κατακόρυφες κινήσεις είναι ημιτονοειδή με την ίδια συχνότητα.
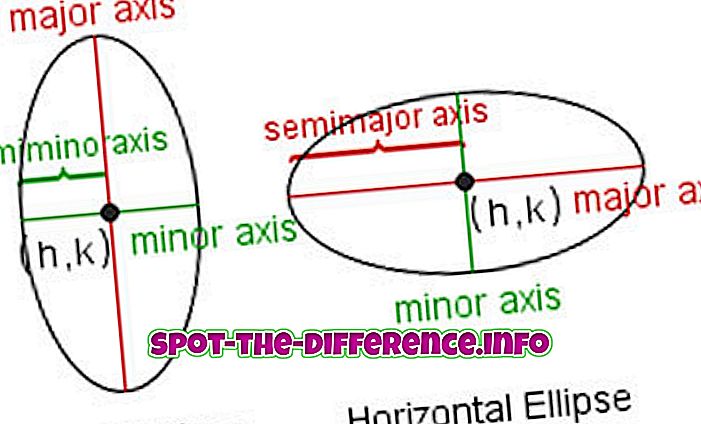
Οι όροι που εμπλέκονται κυρίως στην ορολογία της έλλειψης είναι:
Focus : Η απόσταση από το κέντρο και εκφράζεται με βάση τις κύριες και τις δευτερεύουσες ακτίνες.
Εκκεντρικότητα : Η εκκεντρότητα της έλλειψης (που συνήθως δηλώνεται ως είτε ε είτε ε) εκφράζεται σε όρους χρησιμοποιώντας τον παράγοντα επιπέδωσης.
Directrix : είναι μια γραμμή παράλληλη προς τον δευτερεύοντα άξονα και με την οποία συνδέεται κάθε εστίαση.
Latus rectum : Οι χορδές μιας έλλειψης οι οποίες είναι κάθετες στον κύριο άξονα και περνούν μέσα από μία από τις εστίες τους ονομάζονται το ορθό πρωκτό της ελλείψεως.
Κύριος / Μικρός άξονας : Η μεγαλύτερη και μικρότερη διάμετρο ελλιπούς. Το μήκος του κύριου άξονα είναι ίσο με το άθροισμα των δύο γραμμών παραγωγής.
Ημι-κύριος / ημι-δευτερεύων άξονας : Η απόσταση από το κέντρο στο πιο μακρινό και πλησιέστερο σημείο της έλλειψης. Ο μισός από τον κύριο / δευτερεύοντα άξονα.
Χορδές : Τα μεσαία σημεία μιας δέσμης παράλληλων χορδών ελλειψοειδούς είναι συνθετικά.
Περίμετρος : συνδέεται με το μήκος του ημικυκλικού άξονα και την εκκεντρότητα και αποτελεί αναπόσπαστο τμήμα ελλείψεως.
Σύγκριση μεταξύ κύκλου και ελλείψεων:
Κύκλος | Ελλειψη | |
Ορισμοί | Ένας κύκλος είναι ένας στρογγυλός αεροπλάνο, του οποίου το όριο (η περιφέρεια) αποτελείται από σημεία ίσα από ένα σταθερό σημείο (το κέντρο). | Μια έλλειψη είναι ένα κανονικό σχήμα ωοειδούς, που εντοπίζεται από ένα σημείο που κινείται σε ένα επίπεδο έτσι ώστε το άθροισμα των αποστάσεων από δύο άλλα σημεία (τις εστίες) να είναι σταθερό, ή να προκύπτει όταν ο κώνος κόβεται από ένα πλάγιο επίπεδο, να μην τέμνει τη βάση. |
Παραλλαγές | Οι κύκλοι δεν διαφέρουν ως προς το σχήμα. παραμένουν το ίδιο σχήμα, ακόμα και όταν αλλάζει η όψη. | Οι ελλείψεις ποικίλουν σε σχήμα από πολύ ευρεία και επίπεδη έως σχεδόν κυκλική, ανάλογα με το πόσο μακριά βρίσκονται οι εστίες μεταξύ τους. |
Ακρίβεια ακτίνας | Έχει μια σταθερή ακτίνα σε όλο το σχήμα. | Δεν έχει σταθερή ακτίνα σε όλο το σχήμα. |
Κύρια εξαρτήματα | Ο κύκλος έχει μια ακτίνα, η οποία βρίσκεται στο κέντρο. | Η ελλειψία έχει δύο εστίες, οι οποίες βρίσκονται στα δύο άκρα. |
Περιοχή | π × r ^ 2 Όπου 'r' είναι η ακτίνα του κύκλου. | π × α × β Όπου το 'a' είναι το μήκος του ημι-κύριου άξονα, και το 'b' είναι το μήκος του ημιυπαίθριου άξονα. |
Πρότυπες εξισώσεις | (xa) ^ 2 + (yb) ^ 2 = r ^ 2 | x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1 |
Ομοιότητα | Οι κύκλοι είναι τα μοναδικά σχήματα, από τα οποία προέρχονται τα άλλα σχήματα. | Οι ελλείψεις προκύπτουν επίσης ως εικόνες ενός κύκλου υπό παράλληλη προβολή και των οριοθετημένων περιπτώσεων προοπτικής προβολής. |