Διαφορά κλειδιού: Μια παραβολή είναι μια κωνική τομή που δημιουργείται όταν ένα επίπεδο κόψει μια κωνική επιφάνεια παράλληλη προς την πλευρά του κώνου. Μια υπερβολή δημιουργείται όταν ένα επίπεδο κόψει μια κωνική επιφάνεια παράλληλη προς τον άξονα.

Η παραβολή και η υπερβολή είναι δύο διαφορετικές λέξεις, τομές και εξισώσεις που χρησιμοποιούνται στα μαθηματικά για να περιγράψουν δύο διαφορετικά τμήματα ενός κώνου. Αυτά έχουν διαφορετικό σχήμα, μέγεθος και διάφορους άλλους παράγοντες, συμπεριλαμβανομένων των τύπων που χρησιμοποιούνται για τον υπολογισμό του. Για να τα κατανοήσουμε, ας καταλάβουμε πρώτα τον κώνο και τις διάφορες κωνικές ενότητες.

Ένα κωνικό τμήμα είναι μια καμπύλη που λαμβάνεται όταν ένα επίπεδο τέμνει με κώνο με διάφορους τρόπους. Οι τομές που λαμβάνονται από τη διασταύρωση περιλαμβάνουν έλλειψη, κύκλο, παραβολή και υπερβολή. Σύμφωνα με την αναλυτική γεωμετρία, η κωνική ορίζεται ως "μια επίπεδη αλγεβρική καμπύλη βαθμού 2." Ο δημοφιλής ορισμός της κωνικής ενότητας περιλαμβάνει ένα σημείο εστίασης, γραμμή directrix και εκκεντρικότητα. Το σημείο εστίασης και οι γραμμές directrix αναμένεται να είναι σε σταθερό σιτηρέσιο σε κωνικό. Ο λόγος είναι γνωστός ως η εκκεντρότητα του κωνικού τμήματος. Η εκκεντρότητα των ελλειψιών, παραβολών και υπερβολών διαφέρει. οι ελλείψεις έχουν εκκεντρότητα μικρότερη από 1, οι παραβολές έχουν εκκεντρότητα ίση με 1 και υπερβολές έχουν εκκεντρότητα μεγαλύτερη από 1. Η παλαιότερη γνωστή εργασία σε κωνικές τομές μπορεί να χρονολογηθεί από τον 4ο αιώνα π.Χ. από τον Menaechmus, ο οποίος ανακάλυψε έναν τρόπο για να λύσει το πρόβλημα του διπλασιασμού του κύβου μέσω της χρήσης παραβολών.

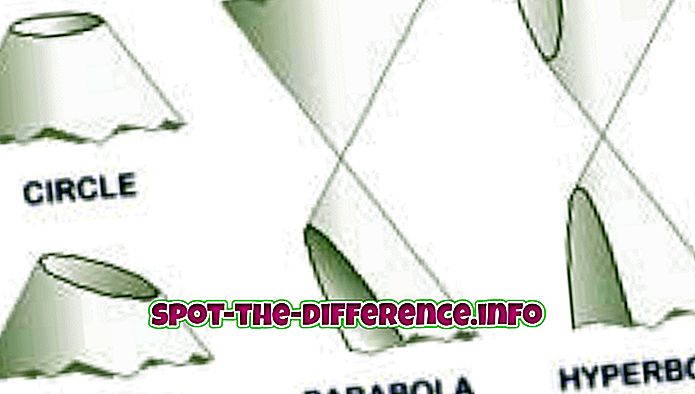
Μια παραβολή είναι μια κωνική τομή που δημιουργείται όταν ένα επίπεδο τέμνει με κώνο. Οι παραβολές ή οι παραβολές σχηματίζονται "από τη διασταύρωση μιας δεξιάς κυκλικής κωνικής επιφάνειας και ενός επιπέδου παράλληλου προς μία ευθεία γραμμή παραγωγής αυτής της επιφάνειας". Ένας άλλος τρόπος δημιουργίας μιας παραβολής είναι όταν ένας τόπος σημείων σε ένα επίπεδο που είναι ισομερώς από την εστίαση και το directrix δημιουργεί μια παραβολή. Στην άλγεβρα, οι παραβολές χρησιμοποιούνται συνήθως σε γραφήματα τετραγωνικών συναρτήσεων, χρησιμοποιώντας τον τύπο y = x ^ 2.

Μια γραμμή που χωρίζει την παραβολή μέσω της μέσης είναι γνωστή ως άξονας συμμετρίας. αυτή η γραμμή είναι επίσης κάθετη προς την κατευθυντήρια γραμμή και περνάει από την εστίαση. Τα σημεία που βρίσκονται στον άξονα συμμετρίας που τέμνουν την παραβολή ονομάζονται «κορυφές». Η απόσταση μεταξύ της κορυφής και της εστίασης είναι γνωστή ως η εστιακή απόσταση. Οι παραβολές μπορούν να ανοίγουν προς οποιαδήποτε κατεύθυνση, συμπεριλαμβανομένων των επάνω, κάτω, δεξιά ή αριστερά. Επίσης ένα κύριο χαρακτηριστικό των παραβολών είναι ότι είναι όλα τα ίδια, αλλά διαφέρουν σε μέγεθος. Μπορούν να επανατοποθετηθούν και να αναδιαμορφωθούν ακριβώς για να χωρέσουν σε οποιαδήποτε άλλη παραβολή. Οι παραβολές χρησιμοποιούνται σε διάφορες εφαρμογές όπως είναι οι ανακλαστήρες προβολέων αυτοκινήτων, ο σχεδιασμός βαλλιστικών πυραύλων κ.λπ. Παίζουν επίσης σημαντικό ρόλο στη φυσική, τη μηχανική, τα μαθηματικά κλπ.

Οι υπερβολές είναι μια ομαλή καμπύλη που συμβαίνει όταν ένα επίπεδο τέμνει τον κώνο παράλληλο στον άξονα y ο οποίος δημιουργεί μια τομή κατά μήκος της πλευράς του κώνου. Μια υπερβολή ορίζεται από τις γεωμετρικές ιδιότητες ή τις εξισώσεις για τις οποίες είναι μια λύση. Ο όρος «υπερβολή» προέρχεται από την ελληνική λέξη που σημαίνει «υπερβολικά" ή "υπερβολικά". Ο όρος πιστεύεται ότι σχεδιάστηκε από τον Απόλλωνιο της Πέργας, ο οποίος συνέβαλε σημαντικά στη μελέτη των κωνικών τμημάτων.

Μια υπερβολή είναι γνωστό ότι έχει κλαδιά που είναι καθρέφτες εικόνες μεταξύ τους και μοιάζουν με δύο άπειρα τόξα. Τα σημεία στα δύο κλαδιά που βρίσκονται πλησιέστερα μεταξύ τους ονομάζονται κορυφές. Η γραμμή που συνδέει τις κορυφές είναι γνωστή ως ο εγκάρσιος άξονας ή ο κύριος άξονας, ο οποίος αντιστοιχεί στη μεγάλη διάμετρο μιας ελλείψεως. Το μέσο του εγκάρσιου άξονα είναι γνωστό ως το κέντρο της υπερβολής. Η εξίσωση μιας υπερβολής είναι γραμμένη ως x2 / a2- y2 / b2 = 1. Οι υπερβολές χρησιμοποιούνται σε διάφορες εφαρμογές στον σημερινό κόσμο συμπεριλαμβανομένου του μονοπατιού που ακολουθείται από τη σκιά του άκρου ενός ηλιακού ρολογιού, το σχήμα μιας ανοικτής τροχιάς. χρησιμοποιείται ως τόξο σε πολλά κατασκευασμένα κτίρια, ως εξισώσεις στα μαθηματικά και στη γεωμετρία, στη φυσική, κλπ.

Οι υπερβολές και οι παραβολές είναι και οι δύο ανοιχτές καμπύλες, που σημαίνει ότι δεν τελειώνουν και συνεχίζουν απεριόριστα στο άπειρο, κάτι που οι ελλείψεις και οι κύκλοι δεν μπορούν να κάνουν.